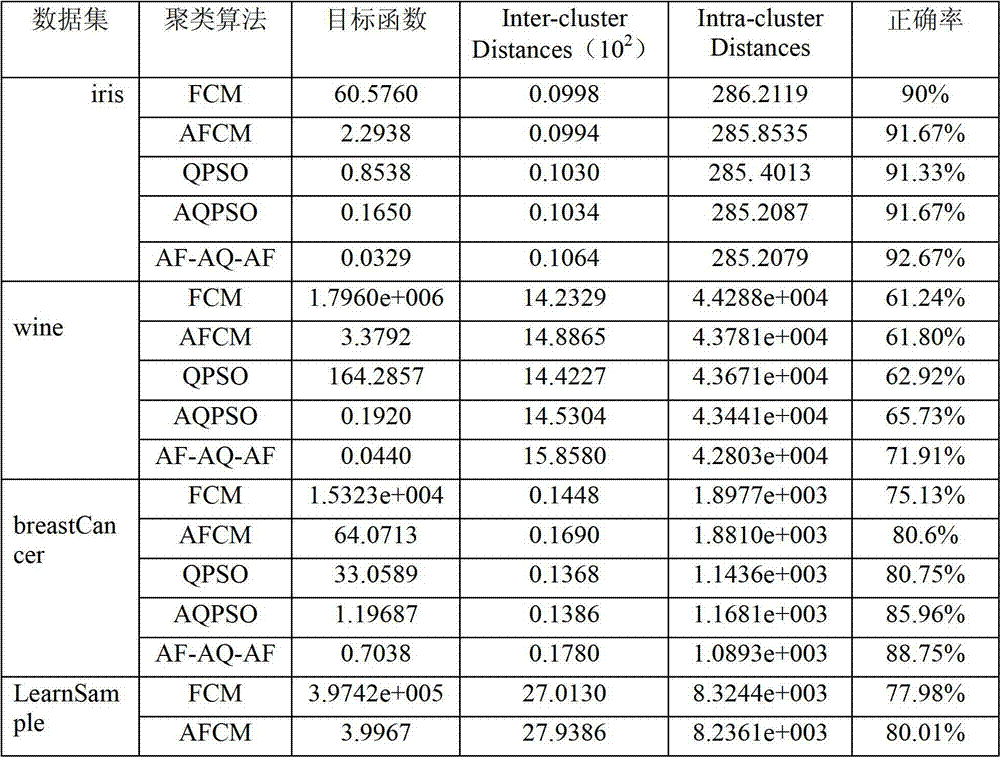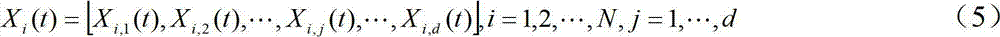
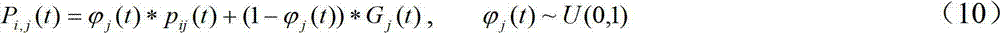
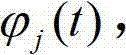 ui,j(t)为符合正态分布的辅助参数;Gj(t)粒子群体的全局最优位置;
ui,j(t)为符合正态分布的辅助参数;Gj(t)粒子群体的全局最优位置; 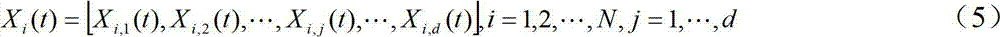
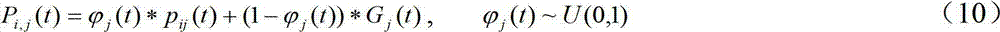
 ui,j(t)为符合正态分布且随机取值的辅助参数,当ui,j(t)>0.5时,公 式(11)中的“±”取-;否则取+,公式(11)中下标j的范围为1到d,Gj(t) 粒子群体的全局最优位置。α是QPSO的收缩扩张系数,它是QPSO收敛的一 个重要参数,对参数α控制可以采用固定取值,或者线性减小的方式。本文采用 α=(1.0-0.5)*(MAXITER-T)/MAXITER+0.5可以达到比较好的效果,其中,MAXITER 是迭代的最大次数,T为当前迭代次数。
ui,j(t)为符合正态分布且随机取值的辅助参数,当ui,j(t)>0.5时,公 式(11)中的“±”取-;否则取+,公式(11)中下标j的范围为1到d,Gj(t) 粒子群体的全局最优位置。α是QPSO的收缩扩张系数,它是QPSO收敛的一 个重要参数,对参数α控制可以采用固定取值,或者线性减小的方式。本文采用 α=(1.0-0.5)*(MAXITER-T)/MAXITER+0.5可以达到比较好的效果,其中,MAXITER 是迭代的最大次数,T为当前迭代次数。