技术领域
本发明属于数字信号处理领域,具体涉及一种基于遗传算法的格型数字滤波器。
技术背景
数字滤波器是数字信号处理系统非常重要的组成部分,是语音与图像处理、模式识别、雷达信号处理、频谱分析等应用中的一种基本的处理部件。一个给定N阶数字滤波器的传递函数H(z)可表示为:
在实时应用中,一个设计好的数字滤波器最终要在一个有限精度的数字器件上实现,而有限字长效应将会大大降低滤波器的性能。众所周知,定点计算与浮点运算相比,具有速度快、存储容量低等优点。短字长的数字滤波器意味着低成本,但精度不高,会使系统性能恶化。因此,尤其在实时性要求较高的场合(如汽车、机器人、雷达、交流电机等),以及在mp4播放器、数字音响、数字彩电等采用专用芯片的大批量生产行业,有限字长效应问题显得尤为突出。
直接型结构最大的优势在于其结构简单,设计好的N阶数字滤波器在直接II转置型结构上实现,则每计算一次输出只需要做2N+1次乘法和N次加法,但所述结构对有限字长的影响非常敏感,从而限制了其应用。而如最佳状态空间实现虽然能够显著的减少有限字长效应,但该实现结构是以提高了滤波器结构的复杂度为代价的。实际上,该结构每计算一次输出一般需要做(N+1)2次乘法和N(N+1)次加法。所以,如何解决结构复杂性和性能之间的矛盾一直是滤波器设计与实现领域中的热点。
格型滤波器结构由于其对有限字长效应具有很强的鲁棒性而被广泛应用于很多实时系统。最初对格型滤波器的研究要追溯到1973年,由Gray和Markel提出了经典的分子抽头式格型滤波器结构,详请参照文献“Digital lattice and ladder filter synthesis”(A.H.Gray,Jr.and J.D.Markrl,IEEE Trans.Audio Electroacoust,vol.AU-21,pp.491-500,Dec.1973),这种结构又被称为Gray-Markel结构。由于所述分子抽头式格型滤波器结构的各个延时器结点后的能量极不均匀,尤其当滤波器的带宽较窄时,Lim在1984年提出了分子注入式格型滤波器,对其存在的缺陷有极大的改善,见文献“On the synthesis of IIRdigital filters derived from single channel AR lattice network”(IEEETrans.Acoust.,Speech,Signal Processing,vol.ASSP-32,no.4,pp.741-749,Aug.,1984)。
但研究表明,一旦给定了数字滤波器的传递函数,所述两种传统的格型滤波器结构参数都是依靠结构而直接确定下来的,往往不能针对特定的性能要求(如灵敏度传递函数、噪声增益等)优化,近期,Li在文献“Very robust low complexity lattice filters”(G.Li,Y.C.Lim,and C.G.Huang,IEEE Trans.Signal Processing.vol.58,no.12,pp.6093-6104,Dec.,2010)中提出一种具有自由度的新型高效简洁格型滤波器结构,该结构集成了所述两种传统格型滤波器结构的优点,结构简单并具有很低的参数灵敏度。但由上述文献可知,该滤波器的优化设计采用全局搜索,当每个注入参数选用一个有符号的2次幂(signpowers of two-SPT)表示时,所述滤波器的设计优化空间包含N(2Ξ+3)N-1个元素,其中正整数Ξ表示参数值能取到的最小分辨率为2-Ξ。该设计方法的搜索空间随阶数N的增长呈指数增长,优化设计效率低,尤其当N较大时,可能导致优化设计失败。虽然优化是离线设计,但过长的设计时间同样也制约了所述滤波器的实际应用。
发明内容
为克服现有技术的上述缺点,本发明提供了一种能够对给定的性能要求进行优化,在得到满足所述性能要求的前提下,提高滤波器的设计效率的基于遗传算法的格型数字滤波器。
基于遗传算法的格型数字滤波器,所述的滤波器由一系列的基本格型单元级联而成,第m级的基本格型单元包括将前向信号fm(n)从后一级单元向前一级单元传输的前向传输工作部和将后向信号bm(n)从前一级单元向后一级单元传输的后向传输工作部;
其特征在于:所述的前向传输工作部包括第一加法器、第二加法器和乘法器,所述的后向传输工作部包括将输入其内的信号存储起来用于下一时刻计算的延时器和第三加法器;
所述的前向信号fm(n)分别输入第一加法器和第二加法器中,前一级单元输出的后向信号bm-1(n)暂存于所述的延时器中;
前向信号与来自延时器的延时信号在第一加法器中相减后形成的减信号,所述的减信号输入乘法器中与比例系数Km相乘、形成比例信号,所述的比例信号输入所述的第二加法器中、与前向信号相加形成当前级的前向输出信号fm-1(n),所述的比例信号输入所述的第三加法器中、与所述的延时信号相加形成当前级的后向输出信号bm(n);
向后一级单元的前向输出信号注入一加权过的输入信号θmu(n)后形成该后一级单元的前向输入信号;
每一级的后向输出信号bk(n)加权一个抽头系数ψk形成加权输出信号ψkbk(n),将所有的基本格型单元的加权输出信号相加形成滤波器的输出信号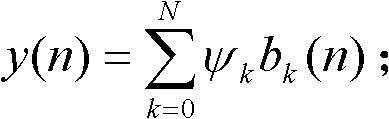
所述的滤波器中还设有能生成注入系数集[θ0,θ1,Λ,θm,Λ,θN],其中θm表示与第m级基本格型单元对应的注入系数的系数生成模块;所述的系数生成模块通过遗传算法获取最优的注入系数集,具体步骤如下:
(1)随机产生Np个注入系数集,将这Np个注入系数集作为当前种群;
(2)根据滤波器需要优化的性能确定适应度函数,计算每个注入系数集的适应度值;
(3)根据适应度值,采用轮盘赌选择法重新选择Np个注入系数集,然后对其进一步交叉、变异,形成新的子代种群;
(4)判断当前世代是否达到最大遗传代数,若是,则进入步骤(5),否则,以步骤(3)形成的子代种群作为当前种群,重复执行步骤(2)-(3);
(5)以适应度值最大的注入系数集作为最优注入系数集输出。
进一步,所述的基本格型单元的前向信号、和后向信号均为经过z变换后的信号,其中:前向信号fm(n)的z变换表示为Fm(z),后向信号bm(n)的z变换表示为Bm(z);所述的第m级基本格型单元的传递函数为: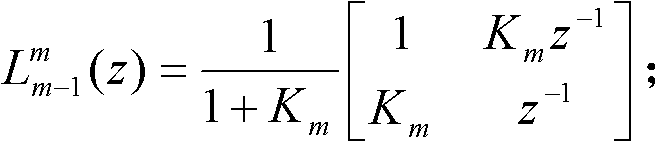
所述的滤波器表示为:
其中:m=1,2,L,N,且θN=0。
本发明的技术构思是:本发明的N阶基本单元格型数字滤波器包括3N+1个乘法器,5N+1个加法器,N个延时器。更加具体地说,该结构由N个基本格型单元级联而成,同时,在每个所述基本格型单元的前向输出信号处注入加权过的输入信号,在其后向输入信号处加权一个抽头系数并输出,需要特别指出的是所述末级基本格型单元的输入为0,输出信号处同样也经加权并输出。然后利用遗传算法针对特定的性能进行优化:首先,根据具体性能要求确定优化的目标函数,以此确定适应度函数;其次,初始化所述结构的注入参数,并确定遗传过程中必须的指标;然后,适应度评价并进行一系列的遗传操作(选择,交叉,变异),遗传过程中判定遗传结束的条件直到遗传完成;最后,根据遗传得到的最优结构得出所述结构的抽头系数。
本发明的有益效果主要表现在:
1.本发明结合所述格型滤波器结构的优点,利用N个具有自由度的加权注入系数,根据具体性能要求对该滤波器结构优化,采用遗传算法节省了大量的搜索时间设计所述性能要求下的最优实现结构参数,这对所述结构的应用推广起到很大的作用;
2.为进一步降低所述格型滤波器结构的实现复杂度,所述加权注入系数可采用SPT表示,由此只需对输入信号进行移位和加法操作便可实现对输入信号的加权,则每计算一次输出便可减少N次乘法,这将大大的降低所述格型结构的实现复杂度;
3.所述遗传算法解决了所述结构不适合设计高阶IIR滤波器的缺点,该算法对该结构的高阶系统应用起到关键的作用。
附图说明
图1是本发明的基本格型单元的结构示意图。
图2是本发明的示意图。
图3是由任意位置的注入信号计算每个状态节点信号的结构示意图。
图4是遗传算法流程图。
具体实施方式
参照附图,进一步说明本发明:
基于遗传算法的格型数字滤波器,所述的滤波器由一系列的基本格型单元级联而成,第m级的基本格型单元包括将前向信号fm(n)从后一级单元向前一级单元传输的前向传输工作部和将后向信号bm(n)从前一级单元向后一级单元传输的后向传输工作部;
所述的前向传输工作部包括第一加法器、第二加法器和乘法器,所述的后向传输工作部包括将输入其内的信号存储起来用于下一时刻计算的延时器和第三加法器;
所述的前向信号fm(n)分别输入第一加法器和第二加法器中,前一级单元输出的后向信号bm-1(n)暂存于所述的延时器中;
前向信号与来自延时器的延时信号在第一加法器中相减后形成的减信号,所述的减信号输入乘法器中与比例系数Km相乘、形成比例信号,所述的比例信号输入所述的第二加法器中、与前向信号相加形成当前级的前向输出信号fm-1(n),所述的比例信号输入所述的第三加法器中、与所述的延时信号相加形成当前级的后向输出信号bm(n);
向后一级单元的前向输出信号注入一加权过的输入信号θmu(n)后形成该后一级单元的前向输入信号;
每一级的后向输出信号bk(n)加权一个抽头系数ψk形成加权输出信号ψkbk(n),将所有的基本格型单元的加权输出信号相加形成滤波器的输出信号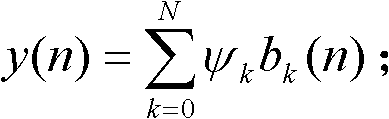
所述的滤波器中还设有能生成注入系数集[θ0,θ1,Λ,θm,Λ,θN],其中θm表示与第m级基本格型单元对应的注入系数的系数生成模块;所述的系数生成模块通过遗传算法获取最优的注入系数集,具体步骤如下:
(1)随机产生Np个注入系数集,将这Np个注入系数集作为当前种群;
(2)根据滤波器需要优化的性能确定适应度函数,计算每个注入系数集的适应度值;
(3)根据适应度值,采用轮盘赌选择法重新选择Np个注入系数集,然后对其进一步交叉、变异,形成新的子代种群;
(4)判断当前世代是否达到最大遗传代数,若是,则进入步骤(5),否则,以步骤(3)形成的子代种群作为当前种群,重复执行步骤(2)-(3);
(5)以适应度值最大的注入系数集作为最优注入系数集输出。
所述的基本格型单元的前向信号、和后向信号均为经过z变换后的信号,其中:前向信号fm(n)的z变换表示为Fm(z),后向信号bm(n)的z变换表示为Bm(z);所述的第m级基本格型单元的传递函数为:
所述的滤波器表示为:
其中:m=1,2,L,N,且θN=0。
本发明的技术构思是:本发明的N阶基本单元格型数字滤波器包括3N+1个乘法器,5N+1个加法器,N个延时器。更加具体地说,该结构由N个基本格型单元级联而成,同时,在每个所述基本格型单元的前向输出信号处注入加权过的输入信号,在其后向输入信号处加权一个抽头系数并输出,需要特别指出的是所述末级基本格型单元的输入为0,输出信号处同样也经加权并输出。然后利用遗传算法针对特定的性能进行优化:首先,根据具体性能要求确定优化的目标函数,以此确定适应度函数;其次,初始化所述结构的注入参数,并确定遗传过程中必须的指标;然后,适应度评价并进行一系列的遗传操作(选择,交叉,变异),遗传过程中判定遗传结束的条件直到遗传完成;最后,根据遗传得到的最优结构得出所述结构的抽头系数。
如图1所示,本发明的基本格型单元包含一个乘法器,三个加法器和一个延时器。如图1所示,对于第m级的基本格型单元,其包含前向传输工作部输入端Fm(z)、后向传输工作部输入端Bm-1(z)和前向传输工作部输出端Fm-1(z)、及后向传输工作部Bm(z)。每来一个时钟信号,信号Fm(z)(即为第m+1级基本格型单元的前向输出信号)与前一时刻存储在z-1里的信号Bm-1(z)相减再经乘法器Km所得到的信号,一方面该信号与原始Fm(z)信号相加得到Fm-1(z)信号,另一方面该信号与所述前一时刻存储在z-1里的信号Bm-1(z)相加得到Bm(z)信号。经计算,所述信号Fm-1(z)、Fm(z)、Bm-1(z)和Bm(z)满足如下关系:
这里,记所述第m级基本格型单元的传递函数为:
如图2所示,fm(n),bm(n)分别为所述新型格型结构的前向、后向信号,它们的z变换分别表示为Fm(z),Bm(z)。所述新型格型结构的主体部分由N个图1所示的基本格型单元级联而成,同时,在每个所述基本格型单元的前向输出信号处注入加权过的输入信号θiu(n),在其后向输入信号处加权一个抽头系数ψk并输出,需要特别指出的是所述末级基本格型单元的输入为0,输出同样也是经过加权的。由此,本发明所述的格型数字滤波器可用以下方程表示:
这里,m=1,2,L,N且θN=0。
每个基本格型单元的后向输入信号bm(n)被存储起来用于下一时刻计算的同时,也是被用来与加权系数ψm相乘合成输出y(n)。对图2的结构示意图进一步的分析分解,图3给出了由任意单个位置的注入信号计算每个状态节点信号的结构示意图。假设输入信号u(n)和bm(n)之间的传输函数为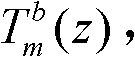 由线性关系可知:
由线性关系可知:
其中,m=1,2,L,N,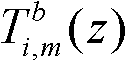 为wi(n)@θiu(n)和bm(n)之间的传输函数(θl=0,
为wi(n)@θiu(n)和bm(n)之间的传输函数(θl=0, )。显然,
)。显然,
接下来根据图3考虑如何计算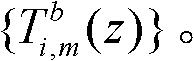
若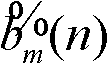 和
和 分别表示bm(n)和fm(n)的值,且:
分别表示bm(n)和fm(n)的值,且:
其中,p=0,1,L,N,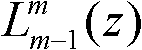 如所述式3定义。图3中的TA(z),TB(z)和TC(z)分别为:
如所述式3定义。图3中的TA(z),TB(z)和TC(z)分别为:
1)当0≤i≤m≤N-1时,
2)当0≤m<i≤N-1时,
对于0≤i≤m≤N-1,由图3可以得到:
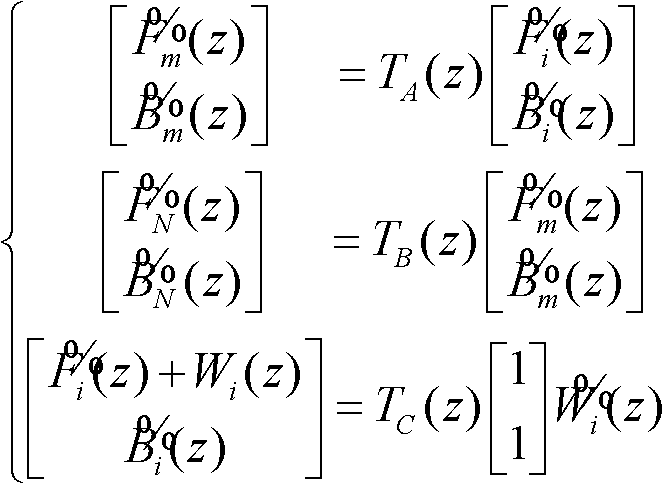 (式10)
(式10)
需要特别指出的是,最后一级输入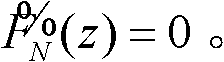
定义
其中,式11的矩阵的四个元素TX(z)都是关于z的函数,为了简化表达,通篇文章中这四个元素的z都将省略不写。
将所述式11带入所述式10,经推导可得:
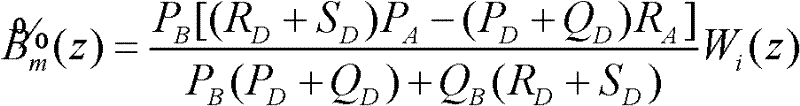 (式12)
(式12)
其中,TD(z)@TA(z)TC(z),因此,
类似地,对于0≤m<i≤N-1,可以得到:
其中,TE(z)=TB(z)TA(z)。
根据图1,图2及图3的分析说明,可以得出所述新型格型结构的参数之间的关系并由此计算之。
所述Bm(z)可表示为: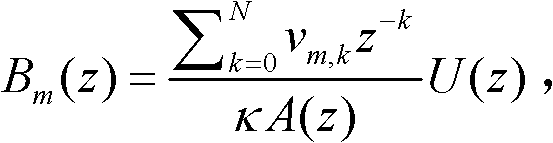 且
且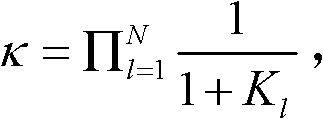 因为
因为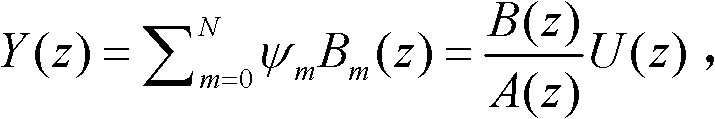 所以,
所以,
假设,Vb=[b0L bkL bN]T,Vψ=[ψ0L ψkL ψN]T,Vm=[vm,0L vm,kL vm,N]T,Mb=[V0L VmL VN]T。结合所述式15可以得到:
因为Mb由所述{Kl}和所述{θk}决定,当给定H(z)时,所述{ψm}是仅关于所述{θk}的函数,即所述{ψm}由所述{θk}唯一确定,当给定需要优化设计的性能要求时,图4给出了所述结构优化的遗传算法的流程图。详细步骤如下:
步骤1:初始化种群-----随机产生Np个种群,其中每个参数θk用Nbbits编码,此时,产生的初始化种群用矩阵Θ表示,其维数为Np×(Nb×N);
步骤2:适应度评估-----根据优化的性能要求确定适应度函数为,并计算相应的适应度值,简称适值;
步骤3:遗传操作-----完成遗传过程中的选择、交叉、变异部分,此时,采用最为常用的轮盘赌选择法选择,多点和均匀相结合的交叉方法,然后再变异;
步骤4:判断-----判断是否达到最大遗传代数,若是,则转至步骤5,若否,则种群更新并转至步骤2;
步骤5:停止进化,根据遗传得到的最优结构得出所述结构的抽头系数。
仿真实例
针对以上介绍的结构及方法,下面就给定一个性能要求优化所述格型结构举一例子。
众所周知,滤波器中的延时器z-1用来存储下一个时钟周期所需的信号数据。输入信号的幅度必须进行归一化,以使所有延时器的字长利用最大化,但同时要防止其过大而产生溢出。理想情况下,所有延时器中信号的幅度应该相等,否则延时器中重要的小幅度信号就不能得到有效的表示而丢失,这将会降低该滤波器的输出性能。因此,状态信号功率比最小化有着重要的实际意义。本例将把滤波器结构的各个状态信号功率比作为结构优化的主要性能指标。
由分析可知,所述状态变量bm(n)是关于自由参数θk的函数。因此,可以通过搜索合适的{θk},使bm(n)(0≤m<N)的最大最小信号功率比最小。若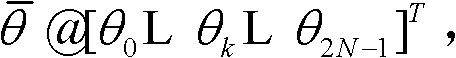 其中T为转置运算符,则状态信号功率比均方值为:
其中T为转置运算符,则状态信号功率比均方值为:
其中, 表示输入信号为高斯白噪声时第m个状态变量bm(n)的方差。理想情况下,
表示输入信号为高斯白噪声时第m个状态变量bm(n)的方差。理想情况下,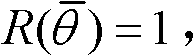 即意味着所有的状态变量可以用相同的位数表示。
即意味着所有的状态变量可以用相同的位数表示。
注意到所述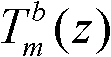 为u(n)和bm(n)之间的传递函数,令
为u(n)和bm(n)之间的传递函数,令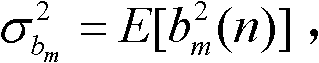 则
则
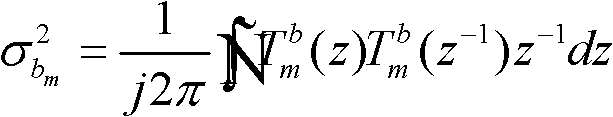 (式18)
(式18)
根据所述式6可得:
其中,
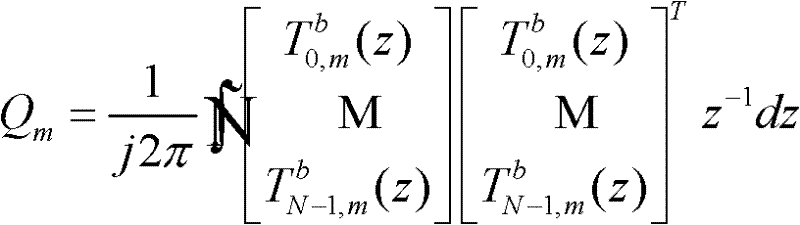 (式20)
(式20)
可以看出,在给定滤波器传递函数时,所述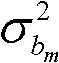 仅取决于{θk}的值。
仅取决于{θk}的值。
为了降低所述格型滤波器结构的实现复杂度,θk采用SPT表示,本例规定Ξ=3,则SPT的空间为:{±2-3,±2-2,±2-1,0,±1},再规定每个参数最多可用两位SPT表示,则每个参数所代表的乘法器就可以用移位和一个加法器替代,这样便可大大的降低所述滤波器结构的实现复杂度。最优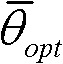 可通过以下目标函数搜索得到:
可通过以下目标函数搜索得到:
给定的理想滤波器可由MATLAB指令ellip(N,rp,rs,ωn)得到,该指令产生一个N阶的低通椭圆滤波器,其中,rp=0.5(dB)是通带波纹,rs=60(dB)是阻带衰减,ωn/2是归一化频率。表1给出了所述理想滤波器的参数。
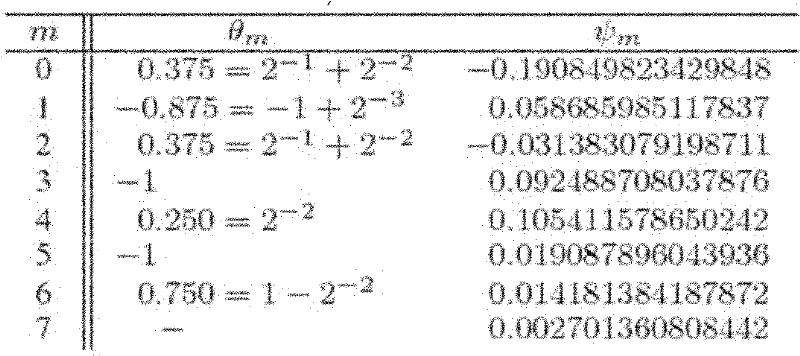
设定初始化种群Np=100,交叉概率pc=0.8,变异概率pm=0.1,Ξ=3及最大递归次数Nr=200,经过遗传算法优化得到所述格型结构的最优注入参数,然后根据所述式16可计算得到抽头系数{ψm},如表2所示。
表1理想滤波器的参数

表2所述格型结构的系统参数
为了验证GA的优化效率,我们同样对Li提出的全局优化方法进行了仿真。针对所述结构的优化特点,总的优化设计时间主要取决于每一次计算式17的时间,也就是取决于搜索空间Θ的大小。假设每计算一次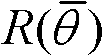 需要的时间为t0,表3给出了两种方法的设计总时间TIME,并给出了对应方法的状态信号最大最小功率比的均方值R。
需要的时间为t0,表3给出了两种方法的设计总时间TIME,并给出了对应方法的状态信号最大最小功率比的均方值R。
表3性能比较
从本例可以看出,本发明具有较低的状态信号功率比,这意味着其具有更强的抗有限字长效应的能力。所述发明的实现只需2N+1个乘法器,并且以其具有自由参数对不同性能要求进行优化的独特优势,有效的解决了结构复杂性和性能之间的矛盾,对实时信号处理系统具有很大的实用价值。
本说明书实施例所述的内容仅仅是对发明构思的实现形式的列举,本发明的保护范围不应当被视为仅限于实施例所陈述的具体形式,本发明的保护范围也及于本领域技术人员根据本发明构思所能够想到的等同技术手段。

