基于粒子群优化算法的神经网络学习优化方法

技术领域

本发明涉及图形学真实感渲染领域，尤其涉及一种基于粒子群优化算法的神经网络学习优化方法。

背景技术

真实感渲染是数字影视制作中非常重要的一部分，也是最耗时的部分。由于渲染一部高质量的作品需要非常长的时间，所以将任务提交到集群内进行并行渲染非常重要，为了能够提高集群的利用效率，需要制定合理的集群作业调度策略，而调度的策略与渲染时间紧密相关，如果能够预测图像渲染的时间对于调度策略的制定帮助很大。

现阶段资源预估的方式主要分为两种：基于硬编码方式的资源预估以及基于历史数据的资源预估。根据资源预估制定合理的调度策略，根据调度策略将任务分派给不同的渲染计算节点来渲染，以此在一定程度上保证集群的负载均衡。

基于硬编码方式的资源预估，首先必须要对整个项目工程有比较深刻的了解，熟知项目的各种处理流程；另外还需要深入研究整个项目的代码编写。通过这些分析后综合分析程序运行过程中可能遇到的所有情况并分析这些情况与时间运行的线性或非线性关系，制定一定的准则进行预估。这种预估方式主要依靠软件代码的编写，在开发过程中就已经设计了专门的模块，但是这种方式灵活性差，很难升级而且不同的环境也不容易操作；结合Renderwing渲染器这种有些特殊的渲染引擎，场景任务的每一小部分都涉及到许多其他部分而且情况繁多，如果单纯以这种方式预估，会非常困难而且准确性也无法保障；而且开发中的系统肯定会不断更新，这种情况也无法更新。所以综合多种情况分析这种预估方式比较适合底层类的开发不适用应用到综合型大工程的资源预估。

基于历史数据的资源预估相对于基于硬编码方式的资源预估，基于历史数据源预估模型考虑如何跳过工程代码比较详细的理解，通过简单分析任务的执行流程以及在大量历史数据的基础上制定一个预估方案，这种方式不需要太多了解软件的编写规则，通过分析学习曾经的历史数据来预估未来需要的资源，达到渲染时间预估的目的。

渲染时间模型这方面的工作较少，2002年Nikolaos Doulamis在文章[Workload Predictionof Rendering Algorithms in GRID Computing]中提出了使用神经网络模型进行渲染负载预估,2004年在文章[A combined fuzzy-neural network model for non-linear prediction of 3Drendering workload in Grid computing]中提出基于神经网络和模糊分类器的基础上进行渲染资源预估；其后AntoniosLitke[Computational workload prediction for Grid oriented industrialapplications:The case of 3D-image rendering]使用人工神经网络算法建立网格基础设施上任务的负载预估模型，并使用3D渲染应用作为实验对象。分析其他工业方向关于时间预估方面的研究大体是基于历史渲染数据，通过数据挖掘技术、统计分析、机器学习和人工智能等方法利用人工神经网络建立时间预估模型。渲染时间预估模型以BP神经网络模型为模板。

神经网络模型是以神经元的数学模型为基础来描述的。神经网络模型由网络拓扑、节点特点和学习规则来表示。神经网络的主要特点为：并行分布处理、高度鲁棒性和容错能力、分布存储及学习能力和能充分逼近复杂的非线性关系。

BP神经网络模型是一种按误差逆传播算法训练的多层前馈网络，能学习和存贮大量的输入-输出模式映射关系，而无需事前揭示描述这种映射关系的数学方程。它的学习规则是使用最速下降法，通过反向传播来不断调整网络的权值和阈值，使网络的误差平方和最小。BP神经网络模型拓扑结构包括输入层、隐层和输出层。

以BP神经网络为目标进行预估模型的预测，但是经过测试训练以及参考一些技术文献发现BP神经网络的一些缺点：

①局部极小化问题：从数学的角度看，传统的BP神经网络是一种局部搜索优化方法，解决的是一个复杂的非线性问题，网络的权重是通过在局部方向逐步改善调整，这将会造成局部最优权值收敛到局部最小值点，导致网络训练失败。BP神经网络初始值一般不同，不同的初始值同时也会导致网络收敛于不同的极小点，这样会使每次神经网络学习完成后的结果也不同。

②网络收敛速度过慢：由于BP神经网络采取梯度下降算法训练网络，它优化的函数又是比较复杂的，因此，不可避免地“之字形”现象，即如果最小值附近比较平坦，算法会在最小值附近停留很久，收敛缓慢，造成了BP算法低效；同时，由于优化的函数是非常复杂的，它会在神经元的输出接近结果时出现一片平坦区，在这块区域输出变化非常小所以误差变化也非常小，但是训练仍在继续，但是过程看起来是停止的；BP神经网络模型中，权值的更新规则是提前赋给神经网络的，不能每次求迭代的更新值，这样的效率也比较低。

发明内容

本发明为了解决上述问题，提出了一种基于粒子群优化算法的神经网络学习优化方法，本方法在基于RenderMan规范的Renderwing渲染系统提供的历史渲染数据的基础上，首先使用主成分分析法规范化输入历史数据获取样本，然后通过分析使用BP神经网络构建的渲染时间预估模型不足的情况下给出了使用粒子群优化算法作为神经网络训练算法的方案，通过后续的时间预估与实际渲染时间对比得到了较好的预估效果。

为了实现上述目的，本发明采用如下技术方案：

一种基于粒子群优化算法的神经网络学习优化方法，包括以下步骤：

(1)选择粒子群优化(PSO)算法的宏观方向参数，表示粒子构造及种群规模；

(2)设置粒子群优化算法的微观方向参数，根据社会搜索和认知搜索更新粒子自身运动；

(3)结合当前参数，使用粒子群优化算法进行训练学习，以使粒子群中的粒子不断靠拢最优粒子；

(4)通过训练完成的神经网络模型对渲染数据进行时间预估，制定集群作业调度策略，以达到减少真实感渲染时间的目的。

所述步骤(1)中，具体方法为：根据具体神经网络模型的输入层、隐层和输出层的神经元个数，得到单个粒子的维度，也为需要训练的数据个数；选择粒子个数，使用集合方式表达粒子。

所述步骤(1)中，单个粒子的维度等于输入层和隐层的神经元个数的乘积与隐层和输出层神经元个数的乘积之和。

所述步骤(1)中，粒子群中的粒子数目取值范围为[10,200]。

所述步骤(2)中，其方法为：每个粒子根据当前粒子本身搜索到的最佳方案和当前情况下所有粒子中搜索到的最佳方案对自身运动进行更新。

所述步骤(2)中，具体方法为：

设Ppbest表示当前粒子本身搜索到的最佳方案，p_pbest＝(p_pbest1,p_pbest2,...,p_pbestN)，其中，Ppbestm表示当前粒子本身在第m维搜索到的最佳方案，m∈[1，N]，N为单个粒子的维度；

Pgbest表示是当前情况下所有粒子中搜索到的最佳方案，p_gbest＝(p_gbest1,p_gbest2,...,p_gbestN)，其中，Pgbestn表示当前情况下第n个训练数据在所有粒子中搜索到的最佳方案，n∈[1，N]，N为需要训练的数据个数；

粒子自身运动更新为：

v_i,t+1＝w×v_i,t+c₁×r₁×(p_pbest,t-x_i,t)+c₂×r₂×(p_gbest,t-x_i,t) 公式(1)

x_i,t＝x_i,t+v_i,t+1   公式(2)

学习因子即C₁、C₂表示的是每个粒子向P_pbest和P_gbest移动的随机加速项的权重：C₁是粒子追踪P_pbest的权重系数，是对自身的认知，称之为认知；C₂是粒子追踪P_gbest的权重系数，是对种群的认知，称之为社会；r₁、r₂是[0,1]区间内均匀分布的随机数，动态的优化学习因子，惯性权重w是认知和社会化搜索的平衡能力；x_i,t为第i个粒子在第t次变化时的位置，v_i,t为第t次变化时的速度，

所述步骤(2)中，为了是社会搜索和认知搜索有相同的比重，将它们设置为相同的值；使它们能够搜索到P_pbest和P_gbest为中心的区域，设置C1＝C2＝2。

所述步骤(2)中，惯性权重的取值方法为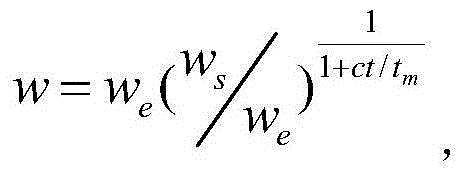：w_s、w_e、t_m分别表示w的初始值、结束值和最大变化次数，此处t与上公式t表示同意含义，t_m可以为最大迭代次数，本文中选取2000，超过2000以后就一直取此数。c为用来平衡社会和认知搜索时间。

惯性权重在[0.5,1]范围内则更倾向于社会化搜索，在[0,0.5)范围内则倾向认知搜索。

认知搜索是指从外界环境获取信息，加工信息，调整自己行为适应环境的搜索方法。社会化搜索是指考虑了社会化因素例如交互，联系，用户行为模式等的网络搜索方法。

所述步骤(3)的具体方法，包括以下步骤：

(3-1)初始化粒子的速度和位置；

(3-2)计算当前粒子本身搜索到的最佳方案和当前情况下所有粒子中搜索到的最佳方案；

(3-3)更新粒子速度与位置；

(3-4)对比当前粒子的适应值与当前粒子本身搜索到的最佳方案和当前情况下所有粒子中搜索到的最佳方案；

(3-5)检测当前情况下所有粒子中搜索到的最佳方案，是否达到条件或迭代次数已达到最大，如果是则输出最优解，完成训练，如果否则返回步骤(3-2)。

本发明的工作原理为：粒子群优化算法(Particle Swarm optimization,PSO)是Eberhart博士和kennedy博士通过模仿鸟群寻食行为而开发出的一种团队合作的随机搜索算法。PSO算法模仿鸟群的寻食过程：鸟群在一个范围内自由寻找食物，在这个范围内仅有一个目标食物；这些鸟都不知道食物的位置，但是他们知道食物距离自身所在地的距离，那么这些鸟通过查找自身周围的鸟群发现离食物近的鸟的方位并朝此方位运行，如此不断地查找直至找到食物。

PSO算法从上述自然界现象得到灵感，并尝试将其用于解决实际问题，由于神经网络的训练时NP问题，求解是简单的，难的是求最优解，PSO将这些解作为粒子群，单个粒子就是单个解。在网络训练中，每次学习每个粒子都会得到一个预估值与现实值的误差并加以处理得到一个值称为适应值，所有的粒子都会比较自身与其他粒子的适应值，并根据最优的适应值与自身的值更新自身的组织结构(即各个参数权重)。

本发明的有益效果为：

(1)使用PSO算法，方法简单，计算方便，求解速度快，适合求解实数问题；

(2)采用PSO算法训练神经网络，一方面，避免了BP神经网络自身易收敛于局部最优解的缺点；另一方面，克服了遗传算法需要做交叉、变异速度慢等缺点。

附图说明

图1为训练样本时间结果分布图；

图2(a)是预测一部分数据后得到的对比数据统计图；

图2(b)是随着渲染时间的增加，预估时间与误差的变化情况图；

图3(a)是两种算法得到的结果与实际的渲染时间的对比图；

图3(b)是两种训练算法得到的结果与实际渲染时间的误差示意图。

具体实施方式：

下面结合附图与实施例对本发明作进一步说明。

粒子群优化算法(Particle Swarm optimization,PSO)是Eberhart博士和kennedy博士通过模仿鸟群寻食行为而开发出的一种团队合作的随机搜索算法。PSO算法模仿鸟群的寻食过程：鸟群在一个范围内自由寻找食物，在这个范围内仅有一个目标食物；这些鸟都不知道食物的位置，但是他们知道食物距离自身所在地的距离，那么这些鸟通过查找自身周围的鸟群发现离食物近的鸟的方位并朝此方位运行，如此不断地查找直至找到食物。

PSO算法从上述自然界现象得到灵感，并尝试将其用于解决实际问题，由于神经网络的训练时NP问题，求解是简单的，难的是求最优解，PSO将这些解作为粒子群，单个粒子就是单个解。在网络训练中，每次学习每个粒子都会得到一个预估值与现实值的误差并加以处理得到一个值称为适应值，所有的粒子都会比较自身与其他粒子的适应值，并根据最优的适应值与自身的值更新自身的组织结构(即各个参数权重)。PSO算法简单，计算方便，求解速度快，适合求解实数问题，本发明算法的主要思想就是利用PSO算法学习神经网络。

神经网络训练后需要确定的权值数为输入层神经元数*隐层神经元数+隐层神经元数*输出层神经元数，所以需要解决的问题就是设计PSO并使用PSO训练神经网络就重新确定这些权重。

PSO算法设计：

为了使PSO能够融入到神经网络中，PSO算法参数的选择十分重要，其中它的参数又分为宏观方向跟微观方向：

⑴宏观，即粒子构造及种群规模：神经网络模型的输入层、隐层、输出层神经元个数分别为m(8)、n(10)、q(1)；由此得出单个粒子的维度N＝m×n+n×q为90，同时N也是需要训练的数据的个数；粒子群中粒子个数大小一般没有标准选择，根据经验取20到40之间，十个粒子对于大部分实际应用已经足够可以获得比较理想的结果,如果问题规范非常大求解难度很大,取值范围可以到一百到两百之间，本发明中选取20作为粒子数。从而得到粒子的表示：p_i＝(x_i1,x_i2,...,x_iN)其中i取值范围为[1,20]。

⑵微观，即粒子运动方面：每个粒子寻优过程中要参考两个值，Ppbest表示当前粒子本身搜索到的最佳方案，Pgbest表示是当前情况下所有粒子中搜索到的最佳方案。粒子根据这两个值进行对自身运动更新；公式(1)、(2)中是其更新公式：

p_pbest＝(p_pbest1,p_pbest2,..,p_pbestN)；p_gbest＝(p_gbest1,p_gbest2,...,p_gbestN)；

v_i,t+1＝w×v_i,t+c₁×r₁×(p_pbest,t-x_i,t)+c₂×r₂×(p_gbest,t-x_i,t)

                                                   公式(1)

x_i,t＝x_i,t+v_i,t+1    公式(2)

上述两个公式中的参数影响收敛速度，比较重要：

学习因子即C₁、C₂表示的是每个粒子向P_pbest和P_gbest移动的随机加速项的权重：C₁是粒子追踪P_pbest的权重系数，是对自身的认知，称之为认知；C₂是粒子追踪P_gbest的权重系数，是对种群的认知，称之为社会。为了是社会搜索和认知搜索有相同的比重，通常将它们设置为相同的值；使它们能够搜索到P_pbest和P_gbest为中心的区域，设置C₁＝C₂＝2。

认知搜索是指从外界环境获取信息，加工信息，调整自己行为适应环境的搜索方法。社会化搜索是指考虑了社会化因素例如交互，联系，用户行为模式等的网络搜索方法。

惯性权重w：惯性权重是认知和社会化搜索的平衡能力，较大的惯性权重更倾向于社会化搜索，惯性权重较小的倾向认知搜索；对于粒子群中的粒子，训练初期应该更适合多关注社会搜索，后期则应该更关注认知搜索，所以惯性权重应该随着时间而不断减小，变化一般选取为从0.9下降到0.4，本发明采用公式(3)来决定w的值。由于PSO算法早期收敛速度快，使用公式(3)可以是粒子比较快的进入认知搜索，同时避免了算法的早熟现象，即过早地收敛于局部最优解。

$$ w=w_e{(w_s/w_e)}^{\frac{1}{1+\mathrm{ct}/t_m}}$$   公式(3)

公式中的w_s、w_e、t_m分别表示w的初始值0.9、结束值0.4、最大变化次数(可以为最大迭代次数，本文中选取2000，超过2000以后就一直取此数)，公式(3)中的c用来平衡社会和认知搜索时间，本发明中选为10；r₁、r₂是[0,1]区间内均匀分布的随机数,动态的优化学习因子，这样PSO算法中的参数设置完成。

确定了PSO算法中的参数，下一步应该使用PSO来完成训练学习过程，步骤如下：

1.初始化粒子的速度和位置；

2.计算pbest和gbest；

3.根据公式更新速度位置；

4.计算当前粒子的适应值与pbest、gbest对比；

5.检测gbest是否达到条件或迭代次数已达到最大，如果是则输出最优解，完成训练，如果否则返回步骤2。

通过PSO的算法可以看到学习过程中，粒子群中的粒子一直在观察局部最优以及全局最优的粒子，并且不断靠拢，最后达到要求完成训练。

实施例一：

实施例一主要描述了粒子群优化算法如何作为神经网络学习算法训练神经网络的，并通过与构建的预估模型的迭代次数、预估结果的对比进行预估评测。针对这两方面的对比，首先采用的样本集合是一些比较常见的综合场景，场景的渲染时间从几百秒到几千秒不等，大体的时间分布图如图1所示。使用粒子群优化的方法主要就是为了解决BP神经网络收敛过慢以及局部极小的问题，所以重点关注使用PSO算法后的神经网络的学习速度，以训练过程中的迭代次数为说明对象。

首先进行PSO算法参数选择，Ppbest表示当前粒子本身搜索到的最佳方案p_pbest＝(p_pbest1,p_pbest2,...,p_pbestN)，Pgbest表示是当前情况下所有粒子中搜索到的最佳方案p_gbest＝(p_gbest1,p_gbest2,...,p_gbestN)。粒子根据这两个值进行对自身运动更新，更新公式为：v_i,t+1＝w×v_i,t+c₁×r₁×(p_pbest,t-x_i,t)+c₂×r₂×(p_gbest,t-x_i,t)，x_i,t＝x_i,t+v_i,t+1，设置C₁＝C₂＝2。惯性权重公式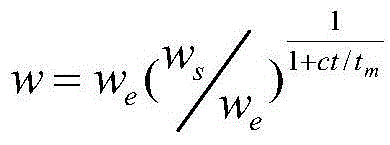：w_s、w_e、t_m分别表示w的初始值0.9、结束值0.4、最大变化次数2000。

确定了PSO算法中的参数，然后使用PSO来完成训练学习过程，步骤如下：

1.初始化粒子的速度和位置；

2.计算pbest和gbest；

3.根据公式更新速度位置；

4.计算当前粒子的适应值与pbest、gbest对比；

5.检测gbest是否达到条件或迭代次数已达到最大，如果是则输出最优解，完成训练，如果否则返回步骤2。

PSO的算法过程中，粒子群中的粒子一直在观察局部最优以及全局最优的粒子，并且不断靠拢，最后达到要求完成训练。

表1中的结果是一次使用PSO训练神经网络的过程，省略去中间的过程，由表中的数据得到本次的训练过程大约迭代了3900次左右，最终的误差小于2E-5。表中avrfit代表所有粒子的平均适应值；bestfit表示最优适应值；gbest则指出了拥有最优适应值的粒子编号；times表示迭代次数。

表1

表2是通过得到的预估模型进行预测得到的数据与实际数据进行的部分对比示例。图2(a)是预测一部分数据后得到的对比数据统计图。图2(b)则比较直观的展示了随着渲染时间的增加，预估时间与误差的变化情况。

表2

综合以上结果，可以看到与BP神经网络预测的结果基本一样随着实际的渲染时间的增加，预估时间与实际时间的数值误差是有增大的趋势，但是该预测点的相对误差(即误差/实际时间)并不一定会增加，而是在一定的范围内浮动。接下来将同样的数据运行在BP神经网络构建的预估模型中，得到结果进行一下比较。对比结果如图3所示。

图3(a)是两种算法得到的结果与实际的渲染时间的对比，图3(b)展示的是两种训练算法得到的结果与实际渲染时间的误差。通过图3(a)、(b)可以发现经由PSO训练产生的预估模型不仅在迭代次数上大大少于直接由BP神经网络产生的预估模型，而且在预估准确度上也并没有太大的差距，反而由图3(b)图发现PSO得到的模型可能更好一些。通过直观上看可能不是太清楚所以我们采用了其他的评价方式：泰尔(THEIL)不等系数即公式(4)。μ取值区间为(0,1)，μ则值越小的预测精度更高。若μ＝0预测值等于序列的实际价值，这是一个理想的情况下，或所谓的完美的预测。与此相反，在μ＝1时，此时示出的预测值和相反的变化趋势的实际值，预测模型显然是不合理的。

$$ \mathrm{\μ}=\frac{\sqrt{\frac{1}{n}\underset{t=1}{\overset{n}{\mathrm{\Σ}}}{(y_t-y_t^{\′})}^2}}{\sqrt{\frac{1}{n}\underset{t=1}{\overset{n}{\mathrm{\Σ}}}{y}_t^2}+\sqrt{\frac{1}{n}\underset{t=1}{\overset{n}{\mathrm{\Σ}}}{y}_t^{\′2}}}$$(y_t为实际值，y′_t为预估值)   公式(4)

通过对两种模型分别对比，发现PSO模型的为μ＝0.0711；BP神经网络直接得到的模型μ＝0.0717，所以通过这样的比较发现经由PSO训练完成的神经网络作为预估模型的效果还是比较不错的。

上述虽然结合附图对本发明的具体实施方式进行了描述，但并非对本发明保护范围的限制，所属领域技术人员应该明白，在本发明的技术方案的基础上，本领域技术人员不需要付出创造性劳动即可做出的各种修改或变形仍在本发明的保护范围以内。