一种认知无线网络中基于双层单调性优化的功率控制方法

技术领域

本发明涉及认知无线电网络中，一种基于双层单调性优化算法而进行的最优功率控制方法。

背景技术

随着移动数据服务的快速增长，可用频谱资源的有限性使得频谱拥塞的问题日益突出。动态频谱接入(DSA)，作为移动网络中传统的固定频谱分配方法的有效补充，通过智能化地重复利用未授权系统(PrimarySystem-PS)或是授权用户(PrimaryUser-PU)充分利用的授权频谱资源，使得非授权用户(SecondaryUser-SU)能够适时地接入PU的授权频谱进行数据传输，从而使得频谱利用率得到有效的提升。DSA以其优越性，被认为是一种能够实现灵活变通的，并且能够响应时下需求的频谱供给方式之典范，前景广阔。然而，DSA网络中进行频谱共享时，在PU服务于SUs的同时会不可避免的产生干扰，其中包括：1)PU与SUs之间的同信道干扰2)不同的SUs之间的相互干扰。为了在保障PU的QoS前提下服务于SUs以获得额外的收益，在设计频谱共享方案的过程中，合理地进行资源分配与干扰管理是非常有必要的。然而以上所述的干扰往往会使得问题具有非凸优化的问题而变得很难解决，因而提出一种在保障PU的QoS同时最大化PU的净收益的有效且高效的优化方法是有意义的。

发明内容

为了保证频谱共享能够优化DSA网络中的频谱资源配置，本发明考虑包括PU与SUs之间以及不同SUs之间的两部分干扰，提出了一种在PU的QoS得到保障的同时，通过最大化PU的净收益以实现最优化的功率控制方法。所提出的功率控制算法具有两层结构，在降低了计算复杂度的同时提高了该方法的有效性以及高效性。

本发明解决其技术问题所采用的技术方案是：

一种认知无线网络中基于双层单调性优化的功率控制方法，所述控制方法包括以下步骤：

(1)在认知无线电网络中，通过授权用户PU和非授权用户SUs的发送功率控制，在考虑包括PU与SUs之间以及不同SUs之间的两部分干扰的同时，保证PU的QoS的情况下最大化PU的净收益的优化问题描述为如下所示的非凸性优化问题：

P1：maxΣ_s∈Ωα_sR_s-β(p₀-p₀^min)

$$ R_s\≥R_s^{req},\∀s\∈\mathrm{\Ω}$$

$$ 0\≤p_0\≤P_0^{max}$$

$$ 0\≤q_s\≤Q_s^{\max },\∀s\∈\mathrm{\Ω}$$

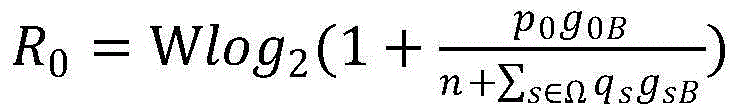其中$$ R_s={\mathrm{Wlog}}_2\left(1+\frac{q_s{g}_{ss}}{n+p_0{g}_{0s}+{\mathrm{\Σ}}_{j\≠s,j\∈\mathrm{\Ω}}{q}_j{q}_{js}}\right),\∀s\∈\mathrm{\Ω}$$表示每个SUs的吞吐量，表示PU的上行链路吞吐量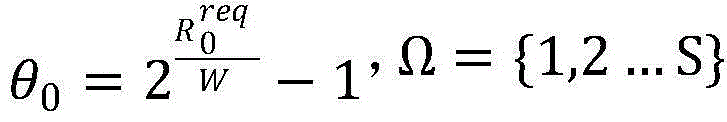，表示的是所有非授权用户(SUs)的集合；

在问题P1中，各个参数定义如下：

α_s:对于每个SUs实现的单位吞吐量PU进行收费的边际系数；

β：PU的边际功率消耗代价，单位为$/Watt；

R_s:每个SUs的吞吐量；

p₀:PU的发送功率；

p₀^min：PU的最小传输功率消耗；

n:背景噪声功率；

q_s:SUs的发送功率；

g_sB:SU-Tx与BS之间的信道功率增益；

g_0B:PU-Tx与BS之间的信道功率增益；

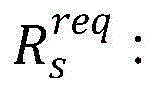每个SUs的吞吐量要求；

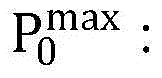PU的发送功率上限；

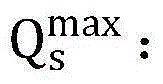SU的最大传输功率上限；

g_0s:PU-Tx与SU-Rxs之间的信道功率增益；

g_ss:SU-Txs与SU-Rxs之间的信道功率增益；

g_js:SU-Txj与SU-Rxs之间的信道功率增益；

W:PU信道的带宽；

参数符号中出现的上标“*”表示参数在优化问题中的最优值；

(2)用公式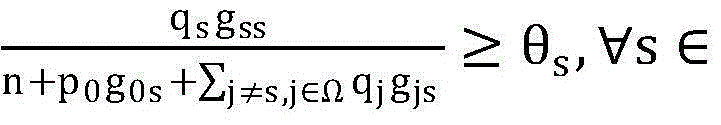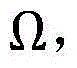$$ R_s={\mathrm{Wlog}}_2\left(1+\frac{q_s{g}_{ss}}{n+p_0{g}_{0s}+{\mathrm{\Σ}}_{j\≠s,j\∈\mathrm{\Ω}}{q}_j{q}_{js}}\right),\∀s\∈\mathrm{\Ω}$$将约束条件中的R_s展开，约束条件的第二项等价于其中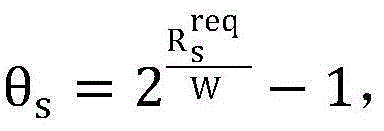问题P1的决策变量就转化为p₀以及{q_s}_s∈Ω，用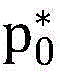和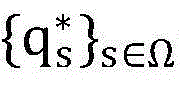分别表示问题P1的最优解；

(3)判断问题(P1)的可行性，将公式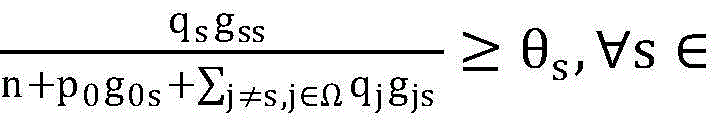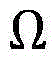中的p₀用{q_s}_s∈Ω代换，从而将该不等式重新表示成如下的一组线性约束：

$$ \left(g_{ss}-\frac{{\mathrm{\θ}}_s{\mathrm{\θ}}_0{g}_{sB}{g}_{0s}}{g_{0B}}\right)q_s-\underset{j\≠s,j\∈\mathrm{\Ω}}{\Σ}\left(\frac{{\mathrm{\θ}}_s{\mathrm{\θ}}_0{g}_{0s}{g}_{jB}}{g_{0B}}\right)q_j$$

$$ \≥{\mathrm{\θ}}_{s}n+{\mathrm{\θ}}_s{\mathrm{\θ}}_0\frac{{\mathrm{ng}}_{0s}}{g_{0B}},\∀s,j\∈\mathrm{\Ω},$$且s≠j

用M表示一个S×S矩阵，S表示Ω中SUs的总数，M中的项表示如下：

此外，还定义S×1的向量u，其中的每一项表示为

$$ u_s=\frac{{\mathrm{\θ}}_s{\mathrm{ng}}_{0B}+{\mathrm{\θ}}_s{\mathrm{\θ}}_0{\mathrm{ng}}_{0s}}{g_{ss}{g}_{0B}-{\mathrm{\θ}}_s{\mathrm{\θ}}_0{g}_{sB}{g}_{0s}},$$

令向量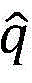表示SUs能够满足上述线性约束条件的传输功率的集合；记条件C1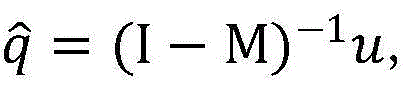：$$ g_{ss}{g}_{0B}-{\mathrm{\&theta;}}_s{\mathrm{\&theta;}}_0{g}_{sB}{g}_{0s}>,\&ForAll;s\&Element;\mathrm{\&Omega;}$$以及条件C2：定义矩阵M的频谱半径，ρ(M)＝max{|λ||λ是M的特征值}，满足ρ(M)<1；如果条件C1与C2能够满足，那么其中I表示S×S的单位矩阵；向量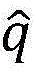即({q_s}_s∈Ω)的每一个元素表示着每个SUs的最小传输功率，SUs的每一项{θ_s}_s∈Ω均满足要求，进一步从{q_s}_s∈Ω中推出PU的最小传输功率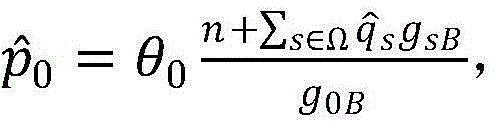然后得到问题P1可行的充分条件即条件C3：

(C3):$$ {\hat{q}}_s\&le;Q_s^{\max },\&ForAll;s\&Element;\mathrm{\&Omega;},$$且$$ {\hat{p}}_0\&le;P_0^{\max }$$

(4)问题(P1)的垂直分层

由于在实现问题P1的优化时总有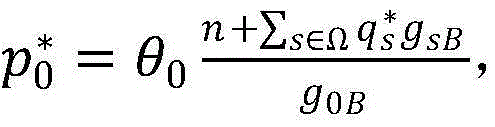也就是说，PU在满足了吞吐量要求的同时无需再消耗更多地传输功率，问题P1垂直分解为两层结构，分别为问题(P1-底层)与问题(P1-顶层)，在底层问题中首先固定PU的传输功率p₀，相应的，底层问题变为在给定PU的传输功率p₀的情况下优化SUs的传输功率q_s；

(P1-底层)：$$ F\left(p_0\right)=\underset{{\left\{q_s\right\}}_{s\&Element;\mathrm{\&Omega;}}}{\max }\underset{s\&Element;\mathrm{\&Omega;}}{\&Sigma;}{\mathrm{\&alpha;}}_s{R}_s$$

$$ 0\&le;q_s\&le;Q_s^{\max },\&ForAll;s\&Element;\mathrm{\&Omega;}$$

$$ \frac{q_s{g}_{ss}}{n+p_0{g}_{0s}+{\mathrm{\&Sigma;}}_{j\&NotEqual;s,j\&Element;\mathrm{\&Omega;}}{q}_j{g}_{js}}\&GreaterEqual;{\mathrm{\&theta;}}_s,\&ForAll;s\&Element;\mathrm{\&Omega;}$$

通过在底层中计算F(p₀)的值，将F(p₀)的值代入到顶层问题从而优化PU的传输功率；

(P1-顶层)：$$ \underset{p_0^{\min }\&le;p_0\&le;p_0^{\max }}{\max }F\left(p_0\right)-\mathrm{\&beta;}\left(p_0-p_0^{\min }\right)$$

其中$$ p_0^{\min }={\mathrm{\&theta;}}_0\frac{n}{g_{0B}};$$

(5)判断问题(P1-底层)的可行性

当p₀确定时，为了满足{θ_s}_s∈Ω，SUs的功率需要能够满足公式$$ \frac{q_s{g}_{ss}}{n+p_0{g}_{0s}+{\mathrm{\&Sigma;}}_{j\&NotEqual;s,j\&Element;\mathrm{\&Omega;}}{q}_j{g}_{js}}\&GreaterEqual;{\mathrm{\&theta;}}_s,\&ForAll;s\&Element;\mathrm{\&Omega;},$$相当于求解方程$$ q_s-{\mathrm{\&Sigma;}}_{j\&NotEqual;s,j\&Element;\mathrm{\&Omega;}}\frac{g_{js}{\mathrm{\&theta;}}_s}{g_{ss}}{q}_j={\mathrm{\&theta;}}_s\frac{n+g_{0s}{p}_0}{g_{ss}},\&ForAll;s\&Element;\mathrm{\&Omega;},$$用N表示一个S×S矩阵，S表示Ω中SUs的总数，N中的项表示如下：

此外，还定义S×1的向量v与向量w，其中的每一项分别表示为

$$ v_s=\frac{{\mathrm{n\&theta;}}_s}{g_{ss}},\&ForAll;s\&Element;\mathrm{\&Omega;}$$

$$ {\mathrm{\&omega;}}_s=\frac{{\mathrm{\&theta;}}_s{g}_{0s}}{g_{ss}},\&ForAll;s\&Element;\mathrm{\&Omega;}$$

因而SUs满足其各自的吞吐量需求{θ_s}_s∈Ω的发送功率表示为

$$ \hat{q}\left(p_0\right)={(I-N)}^{-1}(v+{\mathrm{wp}}_0)$$

当p₀>0时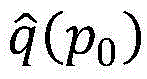，中的项是非负的，看出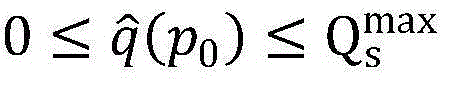时，问题(P1-底层)是可行的；用(x)_s来表示向量x的第s项，将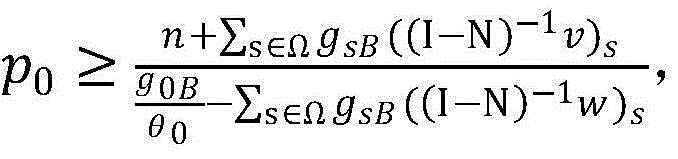$$ \hat{q}\left(p_0\right)=$$$$ {(I-N)}^{-1}(v+{\mathrm{wp}}_0)$$代入不等式$$ p_0\&GreaterEqual;{\mathrm{\&theta;}}_0\frac{n+{\mathrm{\&Sigma;}}_{s\&Element;\mathrm{\&Omega;}}{q}_s{q}_{sB}}{g_{0B}},$$则能够进一步明确问题(P1-底层)在p₀满足不等式该不等式的右边表示p₀的下界，记作P，同时，通过将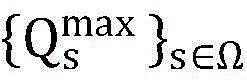$$ \hat{q}\left(p_0\right)={(I-N)}^{-1}(v+$$$$ {\mathrm{wp}}_0)$$与相比较，可求解p₀的上界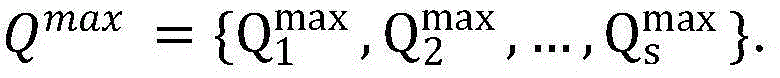，$$ p_0\&le;\underset{s\&Element;\mathrm{\&Omega;}}{\min }\frac{{\left(\left(I-N\right)Q^{\max }-v\right)}_s}{w_s},$$其中Q^max表示S×1的向量，表示为将p₀的上界记为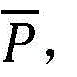因而得出问题(P1-底层)可行的充分条件为

$$ max\{p_0^{\min },\underset{\&OverBar;}{P}\}\&le;p_0\&le;min\{\stackrel{\&OverBar;}{P},p_0^{\max }\}$$

(6)问题(P1-底层)的求解，针对底层问题，采用基于单调性优化的功率控制算法，过程如下：

步骤6.1：引入辅助变量非授权用户的信噪比

$$ y_s=\frac{q_s{q}_{ss}}{n+p_0{g}_{0s}+{\mathrm{\&Sigma;}}_{j\&NotEqual;s,j\&Element;\mathrm{\&Omega;}}{q}_j{g}_{js}},\&ForAll;s\&Element;\mathrm{\&Omega;},$$将底层问题转化为一个关于非授权用户信噪比y_s的单调性优化问题；

$$ \underset{\left\{y_s\right\},s\&Element;\mathrm{\&Omega;}}{max}\underset{s\&Element;\mathrm{\&Omega;}}{\&Sigma;}{\mathrm{\&alpha;}}_s{\log }_2(1+y_s),$$

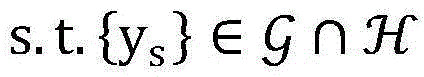
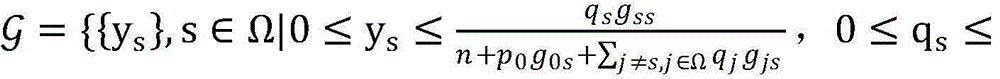
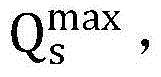
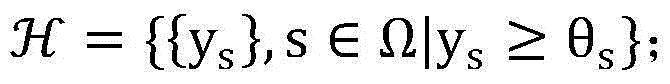
其中$$ {\mathrm{\&Sigma;}}_{s\&Element;\mathrm{\&Omega;}}{q}_s{g}_{sB}\&GreaterEqual;\frac{p_0{g}_{0B}}{{\mathrm{\&theta;}}_0}-n\},$$

步骤6.2：设置初始最优非授权用户信噪比集合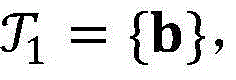其中$$ b_s=\frac{Q_s^{\max }{g}_{ss}}{n+p_0{g}_{0s}},s=1,2,3,...S,$$设置当前的迭代次数k＝1；

步骤6.3：针对当前的最优非授权用户信噪比集合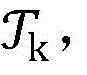计算集合中所有元素的目标函数值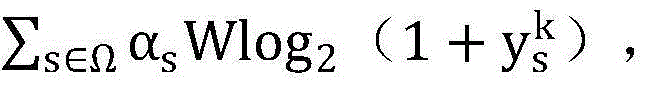记录其中最大的目标函数值对应的点为z^k；

步骤6.4：根据对分法计算原点与z^k的连线与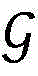的交点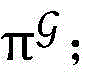

步骤6.5：如果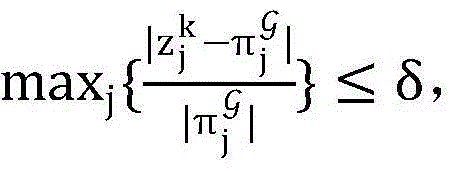则算法终止，转至步骤6.9；否则转至步骤6.6；

步骤6.6：根据公式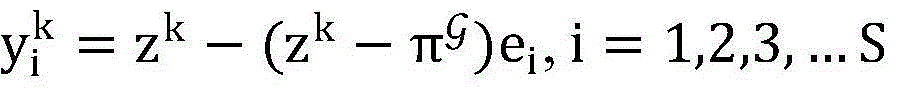计算出S个新的非授权用户信噪比的可选最优解，其中e_i是S个相互正交的单位向量；

步骤6.7：利用步骤6.6中计算出的S个可选最优解代替z^k以更新当前的最优非授权用户信噪比集合，记该集合为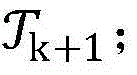

步骤6.8：设置迭代次数k＝k+1，进入下一次循环，返回步骤6.2；

步骤6.9：算法终止，退出算法循环，输出非授权用户信噪比最优解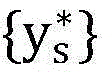为当前集合中目标函数值最大的信噪比；

步骤6.10：根据公式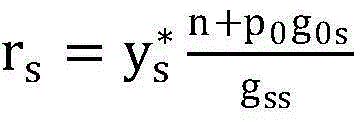设置S维向量r，根据公式q_*＝(I-N)^-1r计算最佳非授权用户发射功率，其中矩阵

步骤6.11：根据公式$$ F\left(p_0\right)={\mathrm{\&Sigma;}}_{s\&Element;\mathrm{\&Omega;}}{\mathrm{\&alpha;}}_s{\mathrm{Wlog}}_2(1+y_s^{*})$$计算在固定p₀的情况下的底层最优目标函数值供顶层使用；

(7)阈值P_th的求解，根据问题(P1-底层)的性质，能够发现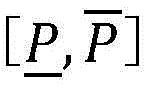上存在一个特殊的阈值P_th，当P≤p₀≤P_th时，不等式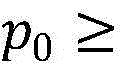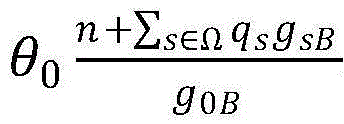才得以成立，因而求解该阈值P_th能够很大程度上缩小最优解的搜索域，求解过程如下：

步骤7.1：初始化设置，设置两个接近于0的很小的正数作为允许的计算误差，分别记为η以及ε，令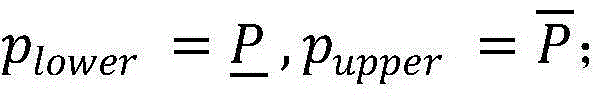

步骤7.2：计算|p_lower-p_upper|,如果该差值比所允许的计算误差ε小，表示所得到的值在误差允许的范围内，则算法终止，跳转至步骤7.6，否则，继续进行步骤7.3；

步骤7.3：将PU的发送功率p₀设置为p_lower与p_upper的中值，即$$ \frac{(p_{lower}+p_{upper})}{2};$$

步骤7.4：由于步骤7.3中给出了p₀，通过步骤6解问题(P1-底层)并且得到相应的最优解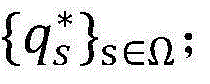

步骤7.5：计算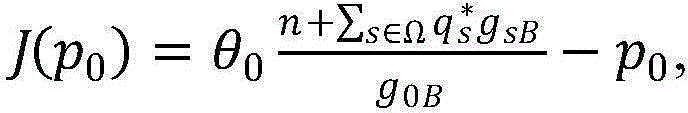用于判断现行的p₀能否满足问题(P1-底层)的约束条件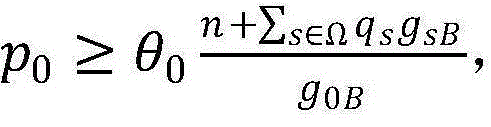因而如果|J(p₀)|<η，则将p₀的上限p_upper更新为现行的p₀，否则将p_lower更新为现行的p₀，返回步骤7.2；

步骤7.6：将所得到的p₀作为特殊阈值P_th；

(8)最大值点Г的求解，进一步根据底层目标函数的单峰特性，基于目标函数的梯度求解函数的最大值点，使得当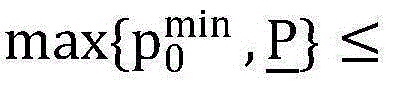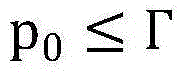时，F(p₀)单调增加，而当p₀≥Γ时，F(p₀)单调减少；求解过程如下：

步骤8.1：初始化设置，设置两个接近于0的很小的正数作为允许的计算误差，分别记为δ以及∈，令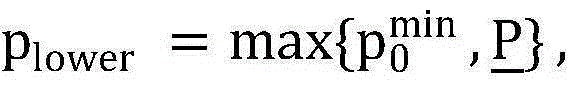p_upper＝P_th，v＝1+∈；

步骤8.2：计算|v|,如果该值比∈小，则算法终止，跳转至步骤8.8，否则，继续进行步骤8.3；

步骤8.3：将PU的发送功率p₀设置为p_lower与p_upper的中值，即$$ \frac{(p_{lower}+p_{upper})}{2};$$

步骤8.4：根据步骤8.3中给出的p₀，通过步骤6解问题(P1-底层)并且得到相应的当前目标函数值F(p₀)，并令f₁＝F(p₀)；

步骤8.5：调用步骤6的底层算法求解f₂＝F(p₀+δ)和f₃＝F(p₀-δ)；

步骤8.6：计算$$ v=\frac{1}{2}(\frac{f_2-f_1}{\mathrm{\&delta;}}+\frac{f_1-f_3}{\mathrm{\&delta;}});$$

步骤8.7：如果v<-∈,则令p_upper＝p₀；否则，如果v>∈,则令p_lower＝p₀；

步骤8.8：算法收敛，输出Γ＝p₀；

(9)问题(P1-顶层)的求解，根据问题(P1-底层)得到的最优解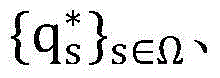最优的目标函数值F(p₀)以及重要的阈值Г，上层问题就转化为一个关于授权用户发射功率p₀的在区间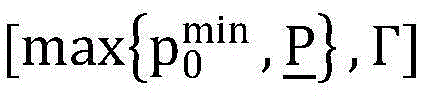上的一维优化问题，采用两维单调性优化算法解问题(P1-顶层)，过程如下：

步骤9.1：引入辅助变量t，使得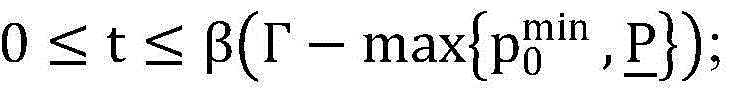$$ \mathrm{\&beta;}(p_0-p_0^{\min })+t=\mathrm{\&beta;}(\mathrm{\&Gamma;}-p_0^{\min }),$$其中t满足条件再引入辅助变量z，使得$$ z=p_0-max\{p_0^{\min },\underset{\&OverBar;}{P}\};$$

步骤9.2：根据辅助变量t与z，将问题(P1-顶层)转化为如下形式的两维单调性优化问题，令x＝(z,t)：

$$ \underset{z,t}{max}F(z+max\{p_0^{\min },\underset{\&OverBar;}{P}\left\}\right)+t-\mathrm{\&beta;}(\mathrm{\&Gamma;}-p_0^{\min })$$

$$ s.t.:0\&le;z\&le;\mathrm{\&Gamma;}-max\{p_0^{\min },\underset{\&OverBar;}{P}\},$$

$$ 0\&le;t\&le;\mathrm{\&beta;}(\mathrm{\&Gamma;}-max\{p_0^{\min },\underset{\&OverBar;}{P}\left\}\right),$$

$$ \mathrm{\&beta;}z+t\&le;\mathrm{\&beta;}(\mathrm{\&Gamma;}-max\{p_0^{\min },\underset{\&OverBar;}{P}\left\}\right).$$

步骤9.3：设置初始最优最优解集合为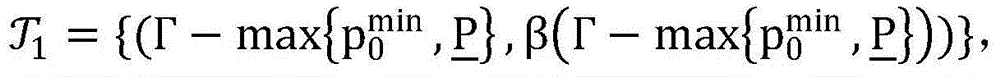设置初始的迭代次数为k＝1，初始的最优解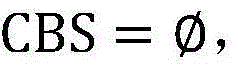初始的最优目标函数值CBV＝-∞；

步骤9.4：计算当前最优解集合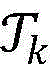中每个点对应的目标函数值记为W(x)，其中需要调用步骤6给出的底层算法；

步骤9.5：删除当前最优解集合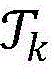中那些满足W(x)≤CBV(1+∈)的所有点，其中∈是一个预先设定的足够小的正数，将余下点的集合记为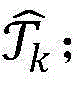

步骤9.6：如果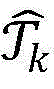为空集，则算法终止，转至步骤9.11；否则继续进行步骤9.7；

步骤9.7：在余下点的集合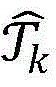中选出目标函数值W(x)最大的点x^cb,k；

步骤9.8：利用对分法计算原点与x^cb,k的连线与外边界的交点y^k；

步骤9.9：如果W(y^k)≥CBV，将最优解更新为CBS＝y^k，CBV＝W(y^k)；

步骤9.10：将x^cb,k从集合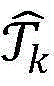中移除，并将两个点{(x^cb,k)₁,(y^k)₂}，{(y^k)₁,(x^cb,k)₂}添加到当前的最优解集合中去，记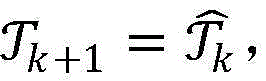k＝k+1，进入下一次循环；

步骤9.11：跳出循环，算法终止，顶层问题的直接最优解(z^*,t^*)＝CBS，然后根据公式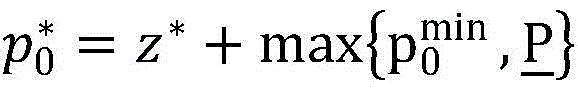求解顶层问题的最优解；

步骤9.12：输出原问题(P1)的最优目标函数值CBV，最优的授权用户发射功率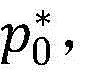最优的非授权用户发射功率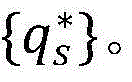

本发明的技术构思为：首先，在考虑认知无线电网络中，授权用户(PU)将自己的频谱共享给非授权用户(SUs)从而获得额外收益的情景。在此处，认为授权用户(PU)需要在保证自己吞吐量的同时服务于非授权用户(SUs)并且分别满足其各自的吞吐量需求，还考虑到授权用户(PU)为了克服相应的干扰从而额外的发射功率花销，同时最大化授权用户(PU)的净收益。接着，通过对该问题的特性进行分析，将该问题转化为两层问题进行求解。然后，根据两层问题的特性，提出基于双层单调性优化的功率控制方法，从而实现在保证PU与SUs吞吐量时PU净收益最大化。

本发明的有益效果主要表现在:1、对于整体系统而言，频谱共享的实施能够通过授权频谱的二次利用，从而提高频谱利用率；2、对于授权用户(PU)而言，在保证自身QoS的同时，能够获得额外的经济收益；3、对于非授权用户(SUs)而言，通过频谱二级市场的交易，能够实现自身的QoS需求，得到满意的服务。

附图说明

图1是认知无线电网络中包含一个授权用户(PU)以及若干非授权用户(SUs)的示意图。

具体实施方式

下面结合附图对本发明作进一步详细描述。

参照图1，一种认知无线网络中基于单调性优化与线性搜索的功率控制方法，实行该方法能在同时满足PU与SUs的前提下，使得PU净收益最大化，同时提高整个系统的频谱资源利用率。本发明应用于认知无线电网络中(如图1所示)。授权用户PU将自己的频谱共享给非授权用户SUs从而获得额外收益的情景。在此处，认为授权用户PU需要在保证自己吞吐量的同时服务于非授权用户SUs并且分别满足其各自的吞吐量需求，还考虑到授权用户PU为了克服相应的干扰从而额外的发射功率花销。针对该问题提出的根据控制发送功率优化系统的方法主要包括步骤如下：

(1)在认知无线电网络中，通过授权用户PU和非授权用户SUs的发送功率控制，在考虑包括PU与SUs之间以及不同SUs之间的两部分干扰的同时，保证PU的QoS的情况下最大化PU的净收益的优化问题描述为如下所示的非凸性优化问题：

P1：maxΣ_s∈Ωα_sR_s-β(p₀-p₀^min)

$$ R_s\&GreaterEqual;R_s^{req},\&ForAll;s\&Element;\mathrm{\&Omega;}$$

$$ 0\&le;p_0\&le;P_0^{max}$$

$$ 0\&le;q_s\&le;Q_s^{\max },\&ForAll;s\&Element;\mathrm{\&Omega;}$$

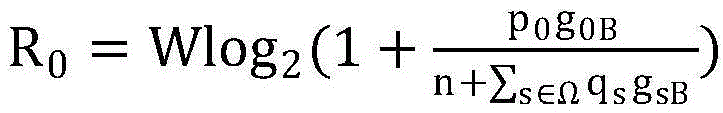其中$$ R_s={\mathrm{Wlog}}_2\left(1+\frac{q_s{g}_{ss}}{n+p_0{g}_{0s}+{\mathrm{\&Sigma;}}_{j\&NotEqual;s,j\&Element;\mathrm{\&Omega;}}{q}_j{q}_{js}}\right),\&ForAll;s\&Element;\mathrm{\&Omega;}$$表示每个SUs的吞吐量，表示PU的上行链路吞吐量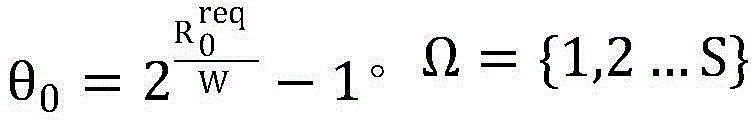，表示的是所有非授权用户SUs的集合。

在问题P1中，各个参数定义如下：

α_s:对于每个SUs实现的单位吞吐量PU进行收费的边际系数；

β：PU的边际功率消耗代价(单位为$/Watt)；

R_s:每个SUs的吞吐量；

p₀:PU的发送功率；

p₀^min：PU的最小传输功率消耗；

n:背景噪声(假设为加性高斯白噪声)功率；

q_s:SUs的发送功率；

g_sB:SU-Tx与BS之间的信道功率增益；

g_0B:PU-Tx与BS之间的信道功率增益；

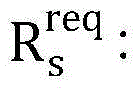每个SUs的吞吐量要求；

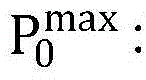PU的发送功率上限；

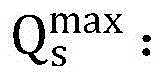SU的最大传输功率上限；

g_0s:PU-Tx与SU-Rxs之间的信道功率增益；

g_ss:SU-Txs与SU-Rxs之间的信道功率增益；

g_js:SU-Txj与SU-Rxs之间的信道功率增益；

W:PU信道的带宽；

注：参数符号中出现的上标“*”表示参数在优化问题中的最优值。

(2)用公式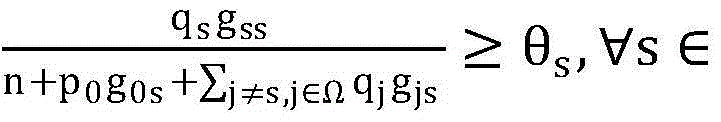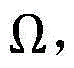$$ R_s={\mathrm{Wlog}}_2\left(1+\frac{q_s{g}_{ss}}{n+p_0{g}_{0s}+{\mathrm{\&Sigma;}}_{j\&NotEqual;s,j\&Element;\mathrm{\&Omega;}}{q}_j{q}_{js}}\right),\&ForAll;s\&Element;\mathrm{\&Omega;}$$将约束条件中的R_s展开，约束条件的第二项等价于其中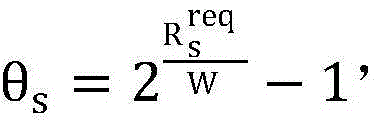问题P1的决策变量就转化为p₀以及{q_s}_s∈Ω，用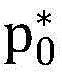和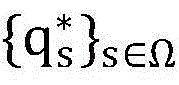分别表示问题P1的最优解；

(3)判断问题P1的可行性。

用M表示一个S×S矩阵，S表示Ω中SUs的总数，M中的项表示如下：

此外，还定义S×1的向量u，其中的每一项表示为

$$ u_s=\frac{{\mathrm{\&theta;}}_s{\mathrm{ng}}_{0B}+{\mathrm{\&theta;}}_s{\mathrm{\&theta;}}_0{\mathrm{ng}}_{0s}}{g_{ss}{g}_{0B}-{\mathrm{\&theta;}}_s{\mathrm{\&theta;}}_0{g}_{sB}{g}_{0s}},$$

令向量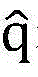表示SUs能够满足线性约束条件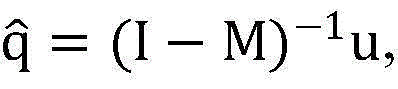$$ (g_{ss}-\frac{{\mathrm{\&theta;}}_s{\mathrm{\&theta;}}_0{g}_{sB}{g}_{0s}}{g_{0B}})q_s-$$$$ {\mathrm{\&Sigma;}}_{j\&NotEqual;s,j\&Element;\mathrm{\&Omega;}}\left(\frac{{\mathrm{\&theta;}}_s{\mathrm{\&theta;}}_0{g}_{0s}{g}_{jB}}{g_{0B}}\right)q_j\&GreaterEqual;{\mathrm{\&theta;}}_{s}n+{\mathrm{\&theta;}}_s{\mathrm{\&theta;}}_0\frac{{\mathrm{ng}}_{0s}}{g_{0B}},\&ForAll;s,j\&Element;\mathrm{\&Omega;},$$且s≠j的传输功率的集合，记条件C1：$$ g_{ss}{g}_{0B}-{\mathrm{\&theta;}}_s{\mathrm{\&theta;}}_0{g}_{sB}{g}_{0s}>0,\&ForAll;s\&Element;\mathrm{\&Omega;}$$以及条件C2：定义矩阵M的频谱半径，ρ(M)＝max{|λ||λ是M的特征值}，满足ρ(M)<1，如果条件C1与C2能够满足，那么其中I表示S×S的单位矩阵，向量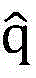即({q_s}_s∈Ω)的每一个元素表示着每个SUs的最小传输功率，SUs的每一项{θ_s}_s∈Ω均满足要求。进一步从{q_s}_s∈Ω(即向量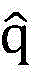)中推出PU的最小传输功率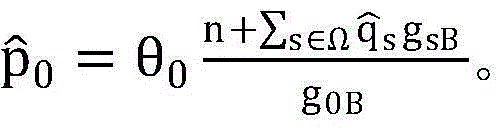然后即可得到问题P1可行的充分条件即条件C3：

(C3):$$ {\hat{q}}_s\&le;Q_s^{\max },\&ForAll;s\&Element;\mathrm{\&Omega;},$$且$$ {\hat{p}}_0\&le;P_0^{\max }$$

(4)问题P1的垂直分层。由于在实现问题P1的优化时总有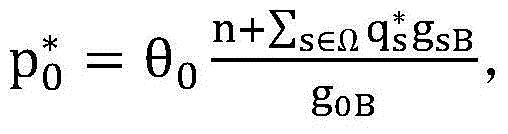也就是说，PU在满足了吞吐量要求的同时无需再消耗更多地传输功率，问题P1垂直分解为两层结构，分别为问题(P1-底层)与问题(P1-顶层)。在底层问题中首先固定PU的传输功率p₀，相应的，底层问题变为在给定PU的传输功率p₀的情况下优化SUs的传输功率q_s。

(P1-底层)：$$ F\left(p_0\right)=\underset{{\left\{q_s\right\}}_{s\&Element;\mathrm{\&Omega;}}}{\max }\underset{s\&Element;\mathrm{\&Omega;}}{\&Sigma;}{\mathrm{\&alpha;}}_s{R}_s$$

$$ 0\&le;q_s\&le;Q_s^{\max },\&ForAll;s\&Element;\mathrm{\&Omega;}$$

$$ \frac{q_s{g}_{ss}}{n+p_0{g}_{0s}+{\mathrm{\&Sigma;}}_{j\&NotEqual;s,j\&Element;\mathrm{\&Omega;}}{q}_j{g}_{js}}\&GreaterEqual;{\mathrm{\&theta;}}_s,\&ForAll;s\&Element;\mathrm{\&Omega;}$$

通过在底层中计算F(p₀)的值，将F(p₀)的值代入到顶层问题从而优化PU的传输功率；

(P1-顶层)：$$ \underset{p_0^{\min }\&le;p_0\&le;p_0^{\max }}{\max }F\left(p_0\right)-\mathrm{\&beta;}\left(p_0-p_0^{\min }\right)$$

其中$$ p_0^{\min }={\mathrm{\&theta;}}_0\frac{n}{g_{0B}}.$$

通过底层问题与顶层问题的交互迭代，最终解决原问题(P1)。需要注意的是，在通过两层算法迭代之前，需要利用步骤3对问题(P1)进行可行性判断，如果条件不满足，整个算法终止，不进行两层算法调用。

(5)判断问题(P1-底层)的可行性，问题(P1-底层)可行的充分条件为

$$ max\{p_0^{\min },\underset{\&OverBar;}{P}\}\&le;p_0\&le;min\{\stackrel{\&OverBar;}{P},p_0^{\max }\}$$

(6)问题(P1-底层)的求解。针对底层问题，采用基于单调性优化的功率控制算法，过程如下：

步骤6.1：引入辅助变量非授权用户的信噪比$$ y_s=\frac{q_s{g}_{ss}}{n+p_0{g}_{0s}+{\mathrm{\&Sigma;}}_{j\&NotEqual;s,j\&Element;\mathrm{\&Omega;}}+q_j{g}_{js}},\&ForAll;s\&Element;\mathrm{\&Omega;},$$将底层问题转化为一个关于非授权用户信噪比y_s的单调性优化问题。

$$ \underset{\left\{y_s\right\},s\&Element;\mathrm{\&Omega;}}{max}\underset{s\&Element;\mathrm{\&Omega;}}{\&Sigma;}{\mathrm{\&alpha;}}_s{\log }_2(1+y_s),$$

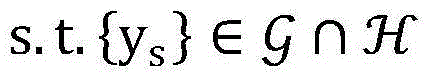
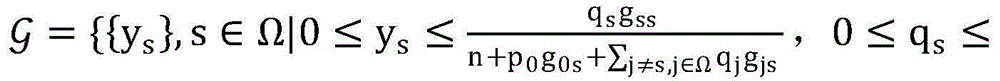
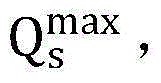
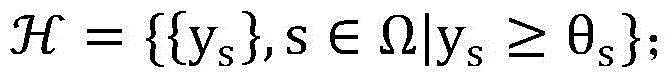
其中$$ {\mathrm{\&Sigma;}}_{s\&Element;\mathrm{\&Omega;}}{q}_s{g}_{sB}\&le;\frac{p_0{g}_{0B}}{{\mathrm{\&theta;}}_0}-n\},$$

步骤6.2：设置初始最优非授权用户信噪比集合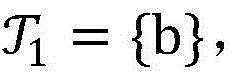其中$$ b_s=\frac{Q_s^{\max }{g}_{ss}}{n+p_0{g}_{0s}},s=1,2,3,...S.$$设置当前的迭代次数k＝1；

步骤6.3：针对当前的最优非授权用户信噪比集合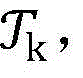计算集合中所有元素的目标函数值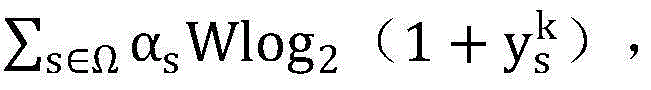记录其中最大的目标函数值对应的点为z^k；

步骤6.4：根据对分法计算原点与z^k的连线与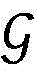的交点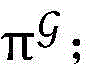

步骤6.5：如果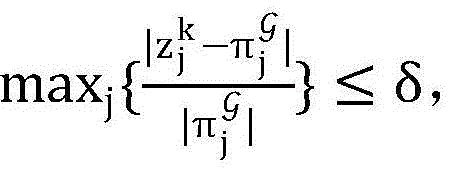则算法终止，转至步骤6.9；否则转至步骤6.6；

步骤6.6：根据公式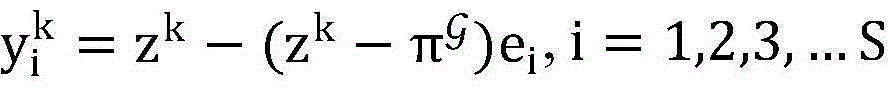计算出S个新的非授权用户信噪比的可选最优解。其中e_i是S个相互正交的单位向量；

步骤6.7：利用步骤6.6中计算出的S个可选最优解代替z^k以更新当前的最优非授权用户信噪比集合，记该集合为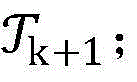

步骤6.8：设置迭代次数k＝k+1，进入下一次循环，返回步骤6.2；

步骤6.9：算法终止，退出算法循环，输出非授权用户信噪比最优解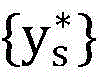为当前集合中目标函数值最大的信噪比；

步骤6.10：根据公式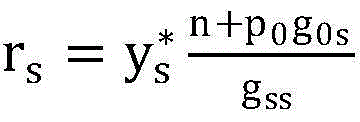设置S维向量r。根据公式q^*＝(I-N)^-1r计算最佳非授权用户发射功率，其中矩阵

步骤6.11：根据公式$$ F\left(p_0\right)={\mathrm{\&Sigma;}}_{s\&Element;\mathrm{\&Omega;}}{\mathrm{\&alpha;}}_s{\mathrm{Wlog}}_2(1+y_s^{*})$$计算在固定p₀的情况下的底层最优目标函数值供顶层使用。

需要注意的是，在采用该基于单调性优化的功率控制算法前，需要根据步骤5进行问题(P1-底层)的可行性判断。如果条件不满足，整个算法终止，不通过此方法进行功率控制。

(7)阈值P_th的求解。根据问题(P1-底层)的性质，能够发现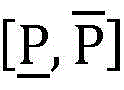上存在一个特殊的阈值P_th，当P≤p₀≤P_th时，不等式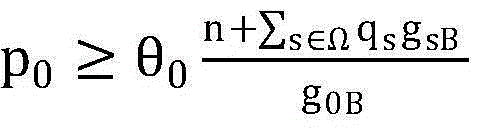才得以成立，因而求解该阈值P_th能够很大程度上缩小最优解的搜索域，求解过程如下：

步骤7.1：初始化设置。设置两个接近于0的很小的正数作为允许的计算误差，分别记为η以及ε。令p_lower＝P,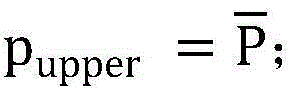

步骤7.2：计算|p_lower-p_upper|,如果该差值比所允许的计算误差ε小，表示所得到的值在误差允许的范围内，，则算法终止，跳转至步骤7.6，否则，继续进行步骤7.3；

步骤7.3：将PU的发送功率p₀设置为p_lower与p_upper的中值，即$$ \frac{(p_{lower}+p_{upper})}{2};$$

步骤7.4：由于步骤7.3中给出了p₀，通过步骤6解问题(P1-底层)并且得到相应的最优解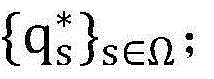

步骤7.5：计算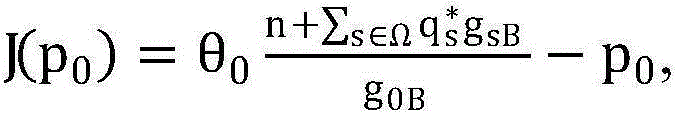用于判断现行的p₀能否满足问题(P1-底层)的约束条件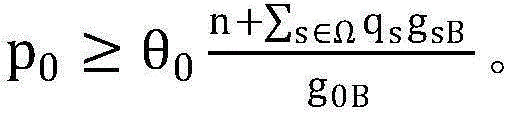因而如果|J(p₀)|<η，则将p₀的上限p_upper更新为现行的p₀，否则将p_lower更新为现行的p₀，返回步骤7.2；

步骤7.6：将所得到的p₀作为特殊阈值P_th；

(8)最大值点Γ的求解，进一步根据底层目标函数的单峰特性，基于目标函数的梯度求解函数的最大值点。使得当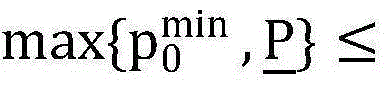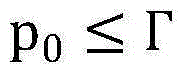时，F(p₀)单调增加，而当p₀≥Γ时，F(p₀)单调减少，求解过程如下：

步骤8.1：初始化设置。设置两个接近于0的很小的正数作为允许的计算误差，分别记为δ以及∈。令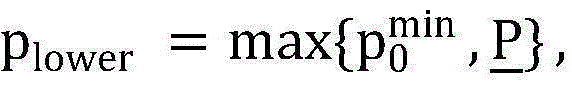p_upper＝P_th，v＝1+∈；

步骤8.2：计算|v|,如果该值比∈小，则算法终止，跳转至步骤8.8，否则，继续进行步骤8.3；

步骤8.3：将PU的发送功率p₀设置为p_lower与p_upper的中值，即$$ \frac{(p_{lower}+p_{upper})}{2};$$

步骤8.4：根据步骤8.3中给出的p₀，通过步骤6解问题(P1-底层)并且得到相应的当前目标函数值F(p₀)，并令f₁＝F(p₀)；

步骤8.5：调用步骤6的底层算法求解f₂＝F(p₀+δ)和f₃＝F(p₀-δ)；

步骤8.6：计算$$ v=\frac{1}{2}(\frac{f_2-f_1}{\mathrm{\&delta;}}+\frac{f_1-f_3}{\mathrm{\&delta;}});$$

步骤8.7：如果v<-∈,则令p_upper＝p₀；否则，如果v>∈,则令p_lower＝p₀；

步骤8.8：算法收敛。输出Γ＝p₀；

(9)问题(P1-顶层)的求解。根据问题(P1-底层)得到的最优解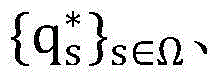最优的目标函数值F(p₀)以及重要的阈值Γ，上层问题就转化为一个关于授权用户发射功率p₀的在区间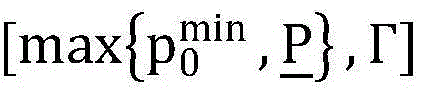上的一维优化问题，采用两维单调性优化算法解问题(P1-顶层)，过程如下：

步骤9.1：引入辅助变量t，使得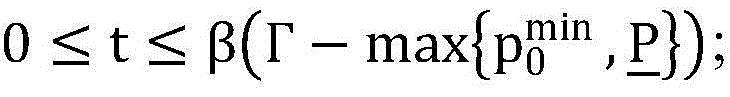$$ \mathrm{\&beta;}(p_0-p_0^{\min })+t=\mathrm{\&beta;}(\mathrm{\&Gamma;}-p_0^{\min }),$$其中t满足条件再引入辅助变量z，使得$$ z=p_0-max\{p_0^{\min },\underset{\&OverBar;}{P}\};$$

步骤9.2：根据辅助变量t与z，将问题(P1-顶层)转化为如下形式的两维单调性优化问题，令x＝(z,t)：

$$ \underset{z,t}{max}F(z+max\{p_0^{\min },\underset{\&OverBar;}{P}\left\}\right)+t-\mathrm{\&beta;}(\mathrm{\&Gamma;}-p_0^{\min })$$

$$ s.t.:0\&le;z\&le;\mathrm{\&Gamma;}-max\{p_0^{\min },\underset{\&OverBar;}{P}\},$$

$$ 0\&le;t\&le;\mathrm{\&beta;}(\mathrm{\&Gamma;}-max\{p_0^{\min },\underset{\&OverBar;}{P}\left\}\right),$$

$$ \mathrm{\&beta;}z+t\&le;\mathrm{\&beta;}(\mathrm{\&Gamma;}-max\{p_0^{\min },\underset{\&OverBar;}{P}\left\}\right).$$

步骤9.3：设置初始最优最优解集合为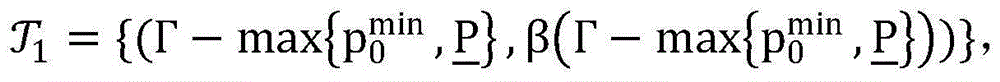设置初始的迭代次数为k＝1，初始的最优解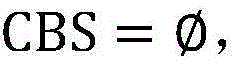初始的最优目标函数值CBV＝-∞；

步骤9.4：计算当前最优解集合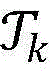中每个点对应的目标函数值记为W(x)，其中需要调用步骤6给出的底层算法；

步骤9.5：删除当前最优解集合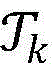中那些满足W(x)≤CBV(1+∈)的所有点，其中∈是一个预先设定的足够小的正数，将余下点的集合记为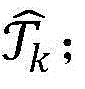

步骤9.6：如果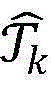为空集，则算法终止，转至步骤9.11；否则继续进行步骤9.7；

步骤9.7：在余下点的集合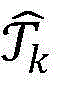中选出目标函数值W(x)最大的点x^cb,k；

步骤9.8：利用对分法计算原点与x^cb,k的连线与外边界的交点y^k；

步骤9.9：如果W(y^k)≥CBV，将最优解更新为CBS＝y^k，CBV＝W(y^k)；

步骤9.10：将x^cb,k从集合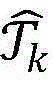中移除，并将两个点{(x^cb,k)₁,(y^k)₂}，{(y^k)₁,(x^cb,k)₂}添加到当前的最优解集合中去，记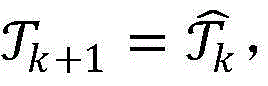k＝k+1，进入下一次循环；

步骤9.11：跳出循环，算法终止。顶层问题的直接最优解(z^*,t^*)＝CBS，然后根据公式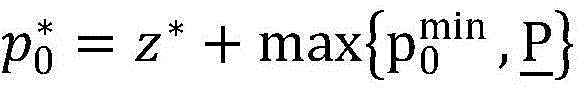求解顶层问题的最优解；

步骤9.12：输出原问题(P1)的最优目标函数值CBV，最优的授权用户发射功率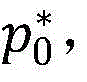最优的非授权用户发射功率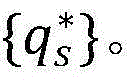

本实施例中，图1是本发明考虑的认知无线电网络中包含一个授权用户(PU)以及若干非授权用户(SUs)的系统。在该系统中，主要考虑的干扰包括两部分：1)PU与SUs之间的同信道干扰2)不同的SUs之间的相互干扰。为了克服由于接入SUs产生的干扰并且满足自身的QoS需求，PU往往需要提升自己的传输功率(与不接入任何SU的情况相比较)，因而SUs端会产生更大的干扰。由于PU的“反干扰”SUs不得不调整自己的传输功率从而满足自己的QoS需求，从而对PU的干扰增大。为了更好地管理该正反馈回路，达到频谱共享的收益，提出了本发明进行问题的解决。

本实施例着眼于在同时满足授权用户PU与非授权用户SUs服务质量的前提下，最大化PU的净收益，激励PU服务SUs，实现系统频谱利用率的提高。的工作使得干扰管理得以用低计算复杂度的方法有效且高效地进行实现。从而能够实现整个系统的频谱资源配置更优化，利用率更高。